 | ♣_______Page mise à jour le 2 janvier 2018 vers 05h20 TUC |
Voici quelques variations à partir du Jeu de la Vie, forme d'automate cellulaire.
Conway a choisi comme règles 23/3 : à chaque nouvelle génération,
- une cellule vivante reste en vie si elle est entourée de deux ou trois voisines gaillardes,
et disparaît dans les autres cas ; - une cellule naît si elle est entourée de trois voisines vaillantes.
On trouvera ici quelques exemples suivant ces règles puis quelques évolutions plus exotiques.
Et vive la vie !
Sommaire
A} En suivant les règles de Conway
B} Quelques variations d'Al Hensel
C} Un vilain petit canard
D} Quelques variations supplémentaires ; et après ?
===================================================A} En suivant les règles de Conway
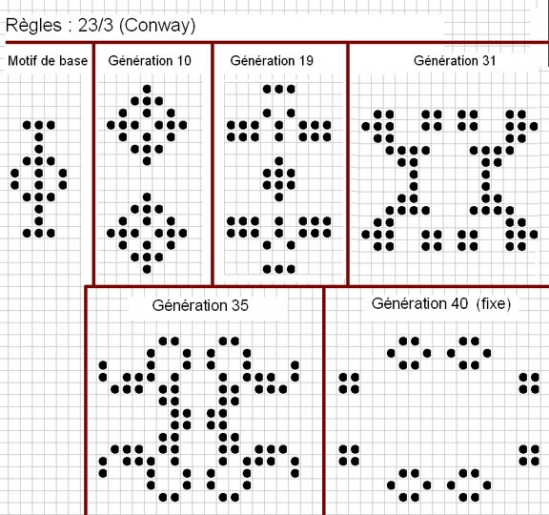 |
|
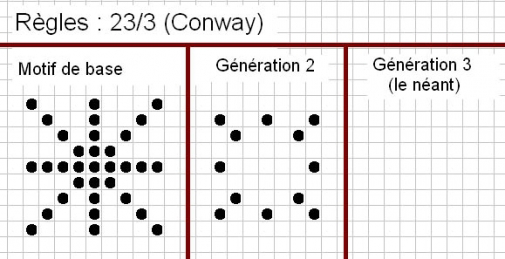
2) Et maintenant, du rapide !
3) Le motif suivant aboutit à un mouvement perpétuel, sur un cycle de quatre générations : 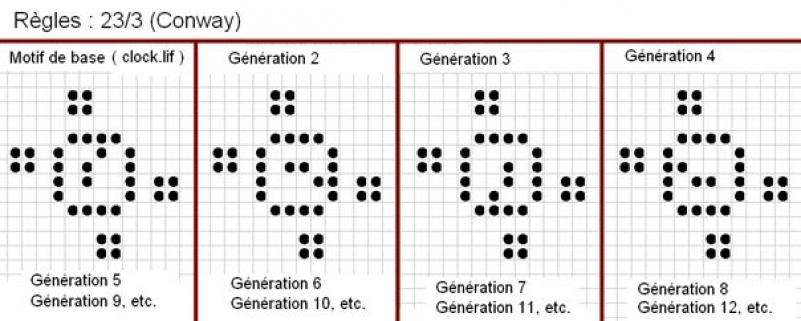
alternant avec une barre horizontale de même longueur.
4) Dernier exemple du lot :
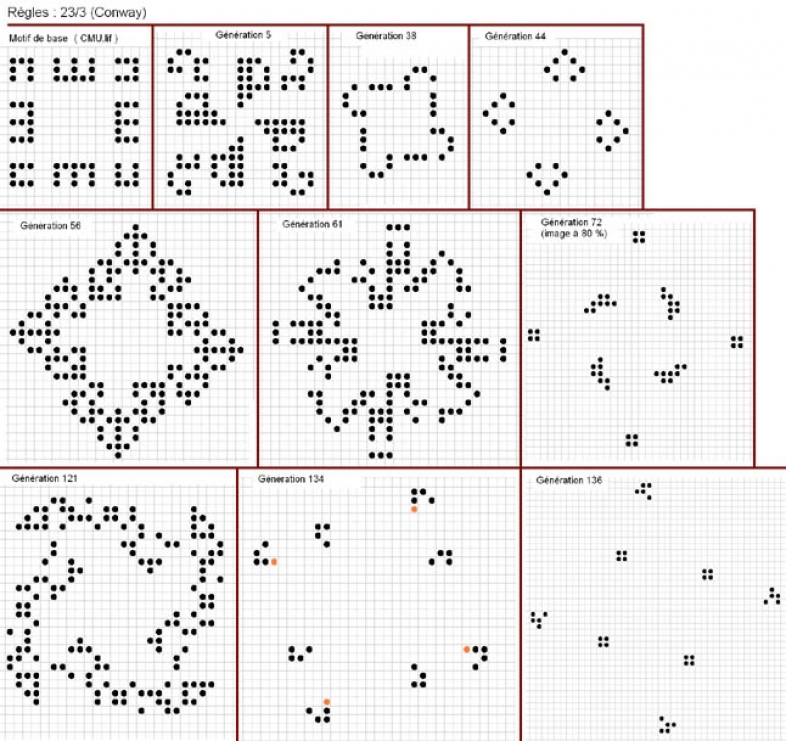
C'est un motif passionnant, autant par ses variations (de soixante-douze cellules au départ à trente-six une fois stabilisé, mais en descendant jusqu'à vingt-huit et montant jusqu'à deux cents) que par sa fin : à la génération 134, restent deux fois quatre groupes, quasiment identiques - seule la cellule orange les différencie ; mais les quatre groupes dépourvus de cette cellule vont aboutir à un carré de deux cellules sur deux (fixe), alors que les quatre autres deviennent des glisseurs : comme dans le motif précédent (la montre), ils suivent un cycle qui les voit retrouver leur forme première toutes les quatre générations, mais en ayant ripé d'une cellule dans l'une des huit directions ; les quatre glisseurs s'éloigneront petit-à-petit du noyau central, agrandissant à l'infini leur univers commun aussi bien que leur solitude propre.
B} Variations proposées par Al Hensel
Trois remarques préliminaires :- La notation 23/3 est bien sûr pure convention, et n'a aucun rapport (c'est le cas de le dire) avec 7,666... Ne serait-ce que parce que 23 n'est pas le nombre vingt-trois mais un ensemble composé de deux éléments : deux et trois ; de ce point de vue, écrire 23, 32 ou 2332232 revient au même.
- Le choix de 23/3 par Conway est-il anthopomorphique ou bien purement pragmatique ? On peut expliquer le choix de 2 3 en disant que si la cellule est trop isolée, elle meurt (vae soli !) et que si elle est trop entourée, elle étouffe ; suffoquer dès quatre voisins semble bien malthusien - mais il est vrai qu'on ne peut jamais en avoir plus de huit. Quant à la (re)génération à trois, pas de commentaire, vu les risques de dérapage. Admettons donc que ces deux règles ont été retenues parce qu'elles semblaient un compromis honnête et produisaient des évolutions intéressantes. Pourtant, on va voir que, si l'on fait abstraction de toute connotation biomorphique, d'autres options ne sont pas moins fécondes.
- Une visite à ConwayLife [⇒] (A community of Conway's Game of Life and related cellular automata ) permettra d'obtenir des informations plus détaillées ; on peut aussi trouver des programmes comme life16.zip d'Al Hensel ou Getalife.zip de Dave Crawford (et d'autres, plus ou moins au goût du jour, applets Java notamment). Jévila [⇒], écrit en VB6, s'essaie à la même tâche.
Voyons donc quelques évolutions obéissant à d'autres règles que celles qu'a retenues Conway.
1) D'abord, quatre ensembles expéditifs...
a}La Mort subite | suivie de | la Grande Invasion : |
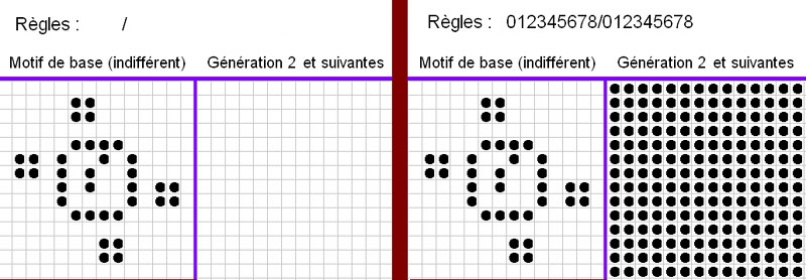
b}Semper idem | puis | le Grand Inverseur : |
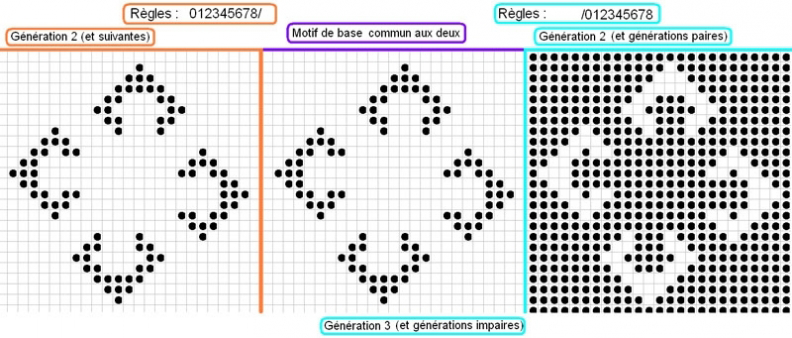
a} des résultats très variables avec /2 :
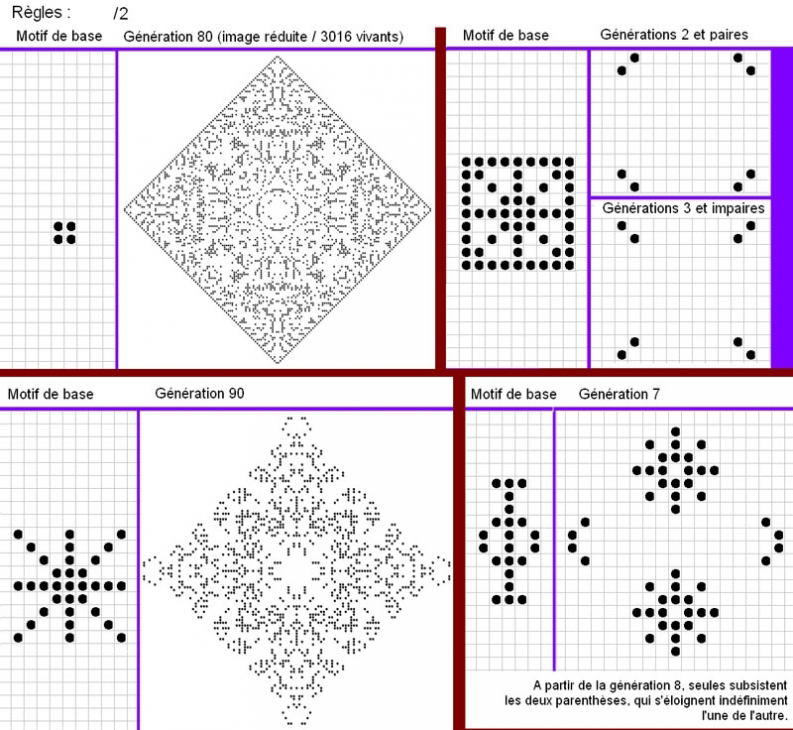
b} une variante du précédent, plus prolifique :
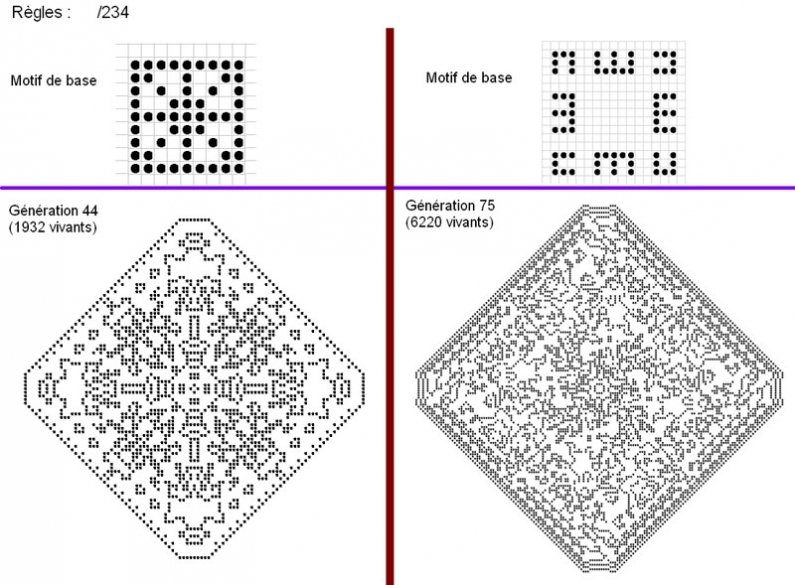
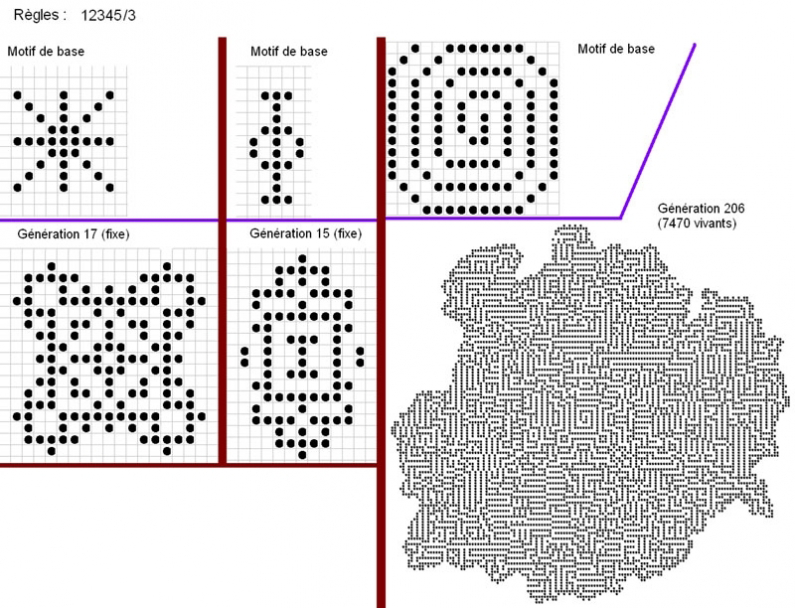
c} Hensel qualifie 12345/3 d'aMAZing : les motifs les plus simples se développent sur une quinzaine de générations
puis se figent ; l'évolution de la spirale est plus surprenante :
C} le vilain petit canard
Si on utilise 23/36 avec la plupart des motifs habituels, c'est un pâle reflet de 23/3, quand ce n'est pas un écran vide au bout d'une dizaine de générations ; mais il y a une exception : une sorte de L (trois cellules en ligne horizontale et trois en ligne verticale, articulées autour d'une cellule vide) ; et là, c'est parti pour un vrai ballet sans limite ; la vidéo présente les premiers ébats de ce motif [cliquer sur ce lien pour afficher le lanceur du clip YouTube ] [⇒].
Son évolution a de quoi fasciner : elle suit un rythme à la fois simple (on retrouve toujours les mêmes formes) et complexe (elles sont en nombre ou disposition variables, à des intervalles sans cesse croissants) ; les tableaux ci-dessous essaient d'en faire apparaître quelques mécanismes, en distinguant
a} le micro-rythme :
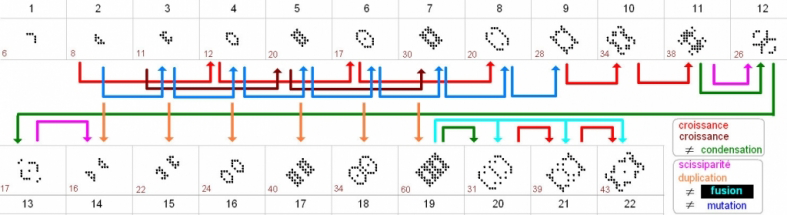
à la base, donc, un cycle de vingt-quatre générations qui se divise en deux demi-cycles de douze, que nous appellerons (par simple commodité de langage) impair pour le premier et pair pour le deuxième ; chaque demi-cycle commence par suivre la même évolution :
- durant les sept premières générations, les motifs grandissent (ou grossissent ou se consolident, selon la métaphore que l'on choisit), mais pas de facon linéaire ; on a deux séries différentes - l'une avec une sorte d'ovale à la paroi mince (voire déchirée), l'autre avec un rectangle aux bords épais ; ce qui est remarquable, c'est que la croissance à l'intérieur de chaque lignée se fait par une succession de transformations de l'une en l'autre ;
- les cinq générations suivantes, elles, ont une évolution différente :
- dans le demi-cycle impair, la consolidation continue sur quatre générations ; la dernière est bouleversifiante (comme aurait dit D. Toscan du Plantier) : le nombre de cellules vivantes chute brusquement pour laisser place à un motif beaucoup plus maigre, mais composé de deux parties distinctes ; la division cellulaire a eu lieu !
- dans le cycle pair, les choses se passent autrement : puisque les sept premières générations reproduisent l'évolution du demi-cycle impair, mais avec un effectif double, à la huitième génération, ce doublement entraîne un contact entre les motifs graphiques qui (nouveau spectacle prodigieux) fusionnent en trois générations ; et dans les deux dernières, les motifs se condensent à nouveau pour ne laisser que des motifs réduits, comme dans le cycle impair, mais en nombre double par rapport à lui.
b} le macro-rythme :
Rappelons que (d'une façon tout-à-fait générale, quels que soient le motif et les règles retenus), un motif de base peut connaître quatre évolutions différentes :
- la fossilisation : à partir de la génération x, plus rien ne bouge, chaque génération étant identique à la précédente ;
- le ludion : à partir de la génération x, les modifications se répètent cycliquement, x se retrouvant à l'identique dans x+2 ou x+3 ou x+n (les étapes intermédiaires étant bien sûr également identiques deux à deux) ;
- Voyager : comme les deux sondes de ce nom, les objets avancent sans fin, s'éloignant toujours plus d'un centre depuis longtemps oublié (et, le plus souvent, fossilisé) ; l'exemple le plus simple en est le glisseur (dont il a été question dans la première partie) ;
- la Genèse (crescite et multiplicamini ) : à chaque génération, la population est plus nombreuse qu'à la précédente, et moins qu'à la suivante ; seules limites : la taille de l'écran - ou celle de la mémoire de l'ordinateur.
Ce qui captive dans l'exemple particulier dont nous parlons ici, c'est qu'on a alternativement Voyager et la Genèse.
Ainsi, aux générations 49, 97, 193, 385, 769, 1537, 3073, 6145, etc. (que appellerons ci-dessous générations Z ), on retrouve exactement le même nombre de cellules vivantes (vingt-quatre) reproduisant le même dessin (deux sortes de chapeaux en miroir), mais la distance entre les deux motifs croît à chaque occurrence ; en cela, nous retrouvons les glisseurs (et Voyager ) ; une différence fondamentale, cependant : la durée entre deux générations Z double à chaque occurrence, parce qu'à chaque fois, il va falloir reconstruire (cycle apres cycle) une sorte de pont entre les deux extrémités - et c'est l'expansion infinie ).

Saluons l'élégance du système, qui n'éloigne pas brutalement les deux chapeaux extrêmes à l'arrivée de chaque générations Z, mais les déplace progressivement de cycle en cycle - et refermons la parenthese pour revenir aux générations Z. Ou plutôt, aux six générations qui précèdent chaque génération Z ; comme cela a été indiqué, le systeme rebâtit, morceau par morceau, l'espèce de pont que l'on peut voir (dans chaque cycle, en plus ou moins complet) aux générations 7 et 19, et (dans toute sa splendeur) aux générations Z-6 ; à la génération 43, on compte cent vingt cellules vivantes ; en 91, deux cent quarante ; en 187, quatre cent quatre-vingts, etc. ; à titre purement indicatif, à la génération 98299, on aura ainsi deux cent quarante-cinq mille sept cent soixante cellules (approximativement la population de Bordeaux), formant huit mille cent quatre-vingt-douze rectangles juxtaposés. Nouveau prodige : quel que soit le nombre de cellules vivantes en Z-6, on se retrouvera avec trente-quatre cellules en Z-1, et vingt-quatre à la prochaine génération Z. En voici un exemple pour les générations 379 à 383 (les dernières à tenir sur mon écran ; les motifs ont été superposés pour rendre le tableau affichable) :
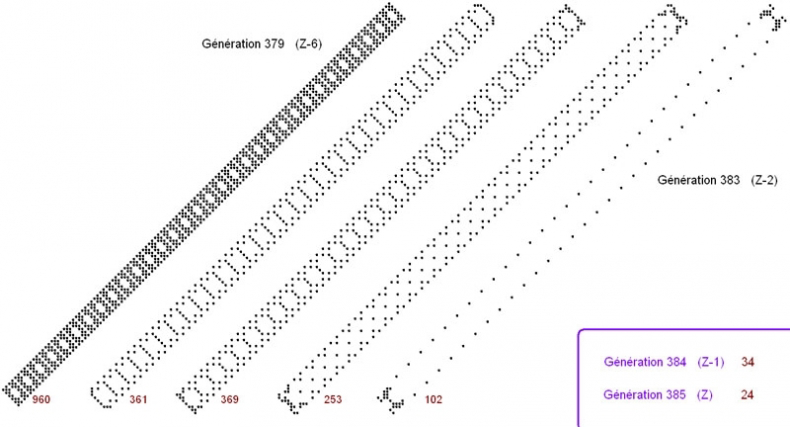
Belle illustration de l'idée stoïcienne de la palingénésie, que Némésios d'Emèse exposait ainsi :
ces astres errants produisent, au bout de périodes de temps bien déterminées, l'embrasement et la destruction de tous les êtres. Puis, lorsque ces astres recommencent de nouveau la même marche, le Monde se trouve reconstitué (citation traduite par P. Duhem, extraite de l'article Eternel retour (temps) de Wikipédia ) ; mais on peut aussi penser à cet idéal que Raymond Queneau fixait à la répétition (considerée comme source du langage) : la même chose avec quelque chose en plus - la même chose, ce sont les deux chapeaux de Z ; le quelque chose en plus, c'est l'espace-temps qui mène d'une génération Z à la suivante, à chaque fois plus vaste, jusqu'à la fin des temps.
Merci, Al !
D- Quelques variations supplémentaires... Et après ?
Mais revenons à plus banal :
1) Parmi les autres trouvailles de Hensel
- un système qui produit des agglomérats dont le cœur est stable, mais la péripherie mobile - un peu à l'image des nuages solaires :
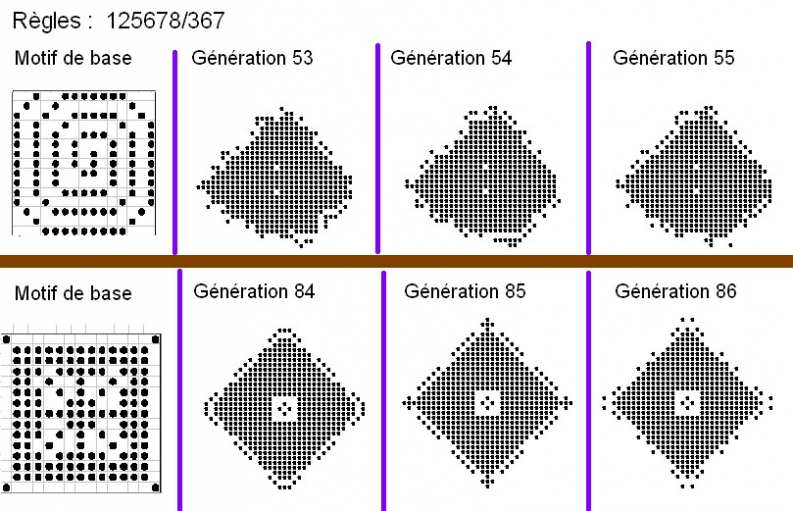
- ci-dessous, en haut, un sous-ensemble du précédent, à déconseiller si vous avez du lait sur le feu : les zones encadrées en vert étaient stables au moment de la capture d'écran, mais reprises par le noyau central par la suite (réduit à dix cellules, à la génération 302) ; il faut donc attendre la 916ème génération pour que l'ensemble se stabilise :
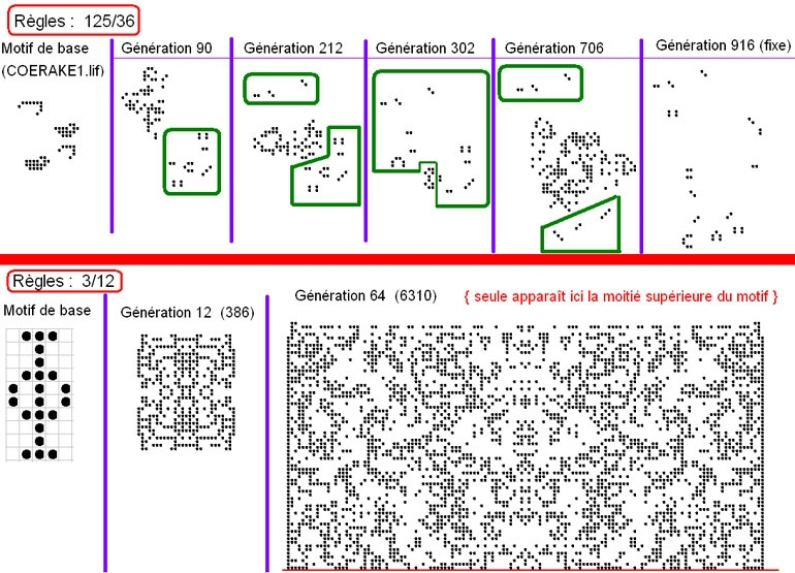
- l'inverse, ci-dessus dans la moitié inférieure : une expansion rapide et sans borne.
Et, pour terminer cette revue,
2) trois systèmes non répertoriés par Al Hensel :
- comme plus haut, une expansion, mais composée de sous-motifs alternant points et petits blocs carrés :
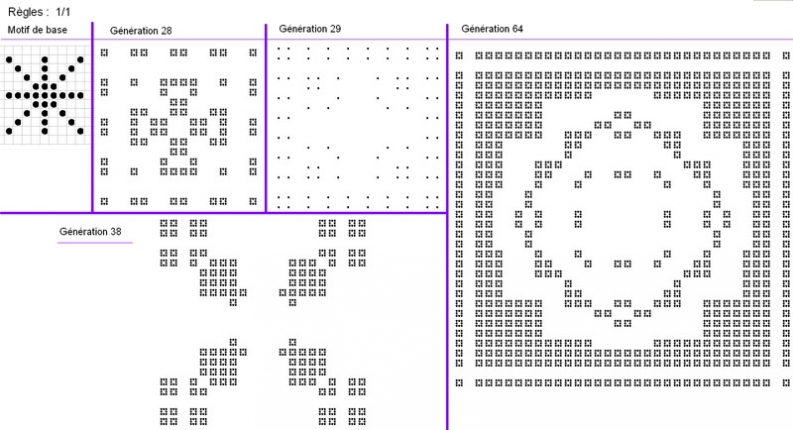
- encore un système en expansion, destiné particulièrement à qui aime les napperons de dentelle en losange :
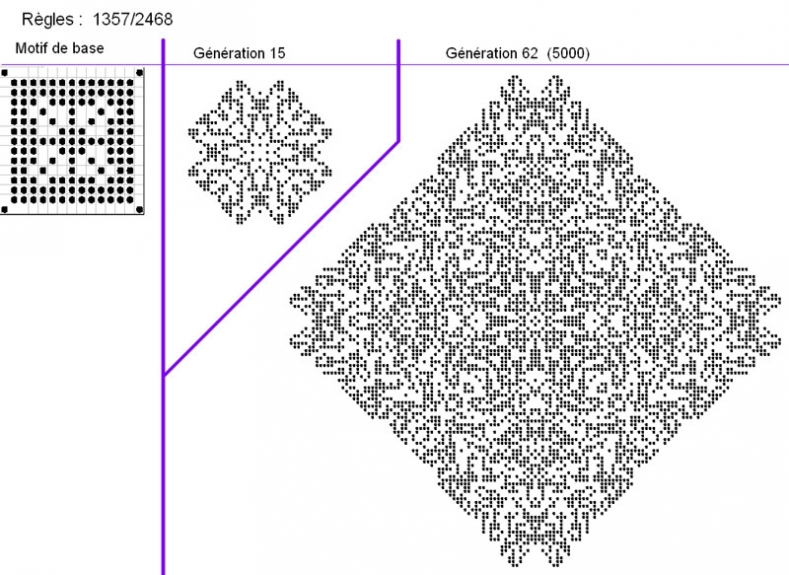
- le dernier, avec des caractéristiques proches des précédents, plus une - plutôt originale - que vous remarquerez certainement :
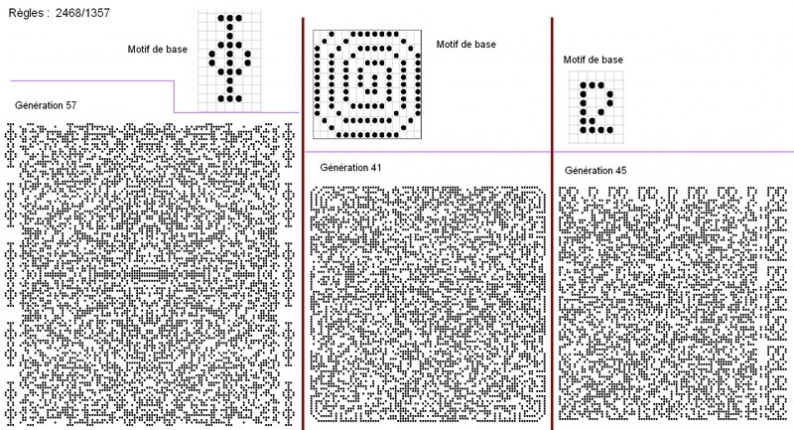
3) Et après ?
Un gadget, en passant : faire choisir au hasard par l'ordinateur les règles qui régissent le passage à la génération suivante - en changeant ces règles à chaque génération ; l'idée aurait sans doute amusé Lewis Carroll (et perturbé Alice un peu plus encore).
Mais au terme de cette promenade dans les allées de John Conway, vers quoi se tourner ? Nous avons laissé le 23/3 pour explorer d'autres terres ; mais la règle de base est restée la même : considérer les huit cellules avoisinantes. Peut-on aller voir ailleurs ?
- d'abord, on pourrait raffiner : dans les règles de notre automate, seul intervient le nombre des cellules ; on pourrait aussi prendre en compte leur disposition, en distinguant par exemple trois cellules en ligne de trois cellules formant un triangle ;
- on pourrait aussi prendre en compte non pas les seules cellules en contact mais toutes celles situées dans une direction (par exemple faire naître une cellule quand x cellules se trouvent alignées dans l'une des huit directions qui en partent) ;
- enfin, le plus naturel : un Jeu de la Vie en trois dimensions, faisant intervenir les vingt (ou vingt-huit) cellules les plus proches ; le codage du jeu ne s'en trouverait pas fondamentalement compliqué, mais comment le traduire visuellement - du moins tant que les PD (*) n'auront pas généralisé l'utilisation du mur holographique en remplacement du vieil écran LED ?
Plan du site & Mentions légales_._Site éclos sur Skyrock, développé avec Axiatel et mûri sur Strato.com_._© 2015-2025 - XylonAkau


